We apply Kirchhoff's Law around the circuit to find that
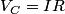 where 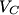 is the voltage across the capacitor. We differentiate this equation with respect to time to obtain is the voltage across the capacitor. We differentiate this equation with respect to time to obtain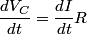 But 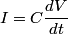 where 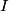 is the current through the capacitor. Actually, because of the sign conventions we have used, is the current through the capacitor. Actually, because of the sign conventions we have used, 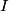 must be replaced by must be replaced by 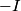 : :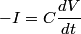 Therefore, 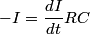 The solution to this equation, with the initial condition that 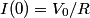 where where 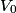 is the initial voltage across the capacitor, is is the initial voltage across the capacitor, is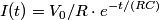 The voltage across the capacitor as a function of time is therefore 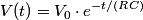 The energy stored in the capacitor is given by 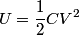 Therefore, the half of the energy is dissipated at a time 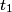 when when 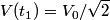 By plugging this into equation (\ref{eqn:1}), we find that 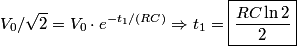 Therefore, answer (E) is correct. |